O mistério dos números 6174 e 495 que intriga matemáticos há 70 anos

Tudo começa com um número qualquer de 4 dígitos, em que ao menos dois sejam diferentes, e, em uma operação de máximo de 7 etapas, você se depara com um enigma.

O número 6174 parece a princípio não ter nada de especial, mas ele intriga matemáticos e entusiastas da teoria dos números desde 1949. Por quê?

Bem, para entender, faça o seguinte:

1. Escolha qualquer número de quatro dígitos que seja composto por pelo menos dois dígitos diferentes, incluindo zero, por exemplo, 1234.

2. Organize os dígitos em ordem decrescente, que em nosso exemplo seria 4321.

3. Agora, organize os números em ordem crescente: 1234

4. Subtraia o menor número do maior número: 4321 - 1234 = 3087

5. E agora repita os últimos três passos

Vamos lá:

Primeiro, organizamos os dígitos em ordem decrescente: 8730. Depois, em ordem crescente: 0378. E subtraímos o menor do maior: 8730 - 0378 = 8352.

Novamente, reorganizamos os dígitos e os subtraímos: 8532 - 2358 = 6174.

Uma vez mais, reordenamos os dígitos e subtraímos: 7641 - 1467 = 6174.

De agora em diante, não vale a pena prosseguir, já que repetiríamos a mesma operação.

• A curiosa origem dos símbolos matemáticos +, - e =
• Como a Índia revolucionou a matemática séculos antes do Ocidente
• Clique para assinar o canal da BBC News Brasil no YouTube

Vamos testar outro número. Que tal 2005?

• 5200 - 0025 = 5175
• 7551 - 1557 = 5994
• 9954 - 4599 = 5355
• 5553 - 3555 = 1998
• 9981 - 1899 = 8082
• 8820 - 0288 = 8532
• 8532 - 2358 = 6174
• 7641 - 1467 = 6174

Assim, não importa com que número começamos, sempre se chegará a 6174.

Um viciado em números

Isto é conhecido como a Constante Kaprekar, batizada em homenagem àquele que descobriu a misteriosa beleza do número 6174 e a apresentou na Conferência Matemática de Madras em 1949, Dattatreya Ramchandra Kaprekar (1905-1986), um viciado confesso na teoria dos números.

"Um bêbado quer continuar bebendo vinho para se manter naquele estado agradável. O mesmo vale para mim quando se trata de números", ele costumava dizer.

Kaprekar era um professor de uma pequena população indiana chamada devlali ou deolali e era frequentemente convidado a falar em outras escolas sobre seus métodos únicos e observações numéricas fascinantes. No entanto, vários matemáticos indianos riam de suas ideias, chamando-as de triviais.

Talvez sejam: é fato que, apesar de a Constante de Kaprekar ser surpreendente e nos levar a suspeitar por trás dela esteja um grande teorema, pelo menos até agora nunca revelou nada.

Aquele que ri por último...

Mas nem tudo tem que ser útil para ser divertido e interessante. Kaprekar se tornou conhecido dentro e fora da Índia, porque muitos outros matemáticos acharam as ideias intrigantes. E, como ele, continuaram brincando com os números.

Yutaka Nishiyama, da Universidade de Economia de Osaka, no Japão, por exemplo, diz na revista +plus que usou um computador para ver se havia um número limitado de etapas para alcançar 6174.

Ele estabeleceu assim que o número máximo de passos é 7, ou seja, se você não alcançar 6174 após usar a operação sete vezes, você terá cometido um erro nos seus cálculos e deverá tentar novamente.

Em outras investigações, descobriu-se que o mesmo fenômeno ocorre quando, em vez de começar com quatro dígitos, começa com três.

Vamos tentar com o número 574?

• 754 - 457 = 297
• 972 - 279 = 693
• 963 - 369 = 594
• 954 - 459 = 495
• 954 - 459 = 495

Como se pode ver, o "número mágico" neste caso é 495.

E não, isso não acontece em outros casos: somente com números de três ou quatro dígitos (pelo menos de 2 a 10 dígitos, que é o que foi testado).

Para estimular os estudantes

Atualmente, a empresa sem fins lucrativos Scigram Technologies Foundation desenvolve na Índia uma plataforma de ensino em computadores especialmente para escolas rurais e tribais. A empresa transformou o número 6174 na tabela colorida que ilustra esta reportagem.

O cofundador Girish Arabale explica que sempre buscam inspirar e motivar aquelas crianças em idade escolar que costumam odiar matemática. "A Constante de Kaprekar 6174 é um desses belos números, e os passos que levam à sua descoberta criam um momento 'aha!', desses que fazem falta nos currículos tradicionais de matemática."

Eles atribuíram, como se pode ver abaixo, uma cor a cada número de etapas necessárias para atingir 6174 (lembre-se que há um máximo de 7 etapas).

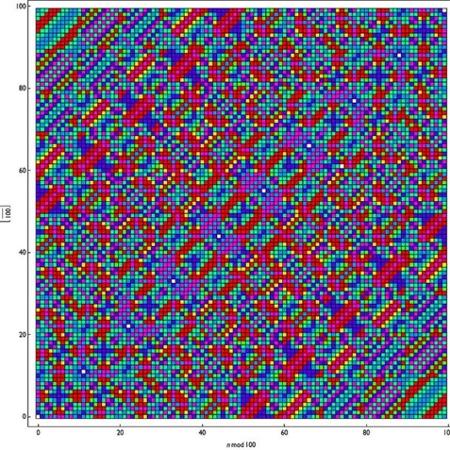
Foi escrito então um código que pode ser facilmente recriado em um Raspberry Pi, computador barato muito usado para ensinar a linguagem Wolfram, disponível gratuitamente no Raspberry Pi. Um programa criou assim padrões com os passos que levam ao número 6174 para cada um dos 10 mil números de 4 dígitos que existem, criando a tabela ao lado com as diferentes cores.

Matemática recreativa

A Constante de Kaprekar não foi o único fruto da paixão do indiano por números. Entre sua coleção de idéias, também está o Número de Kaprekar.

É um número com a interessante propriedade de que, se for elevado ao quadrado e somadas as duas partes iguais do resultado, se chegará ao número original. Para esclarecer, um exemplo:

• 297² = 88.209
• 88 + 209 = 297

Outros casos exemplos de Números de Kaprekar são: 9, 45, 55, 703, 17.344, 538.461... teste e confira!

Mas lembre-se: ao dividir o número cujas partes você vai adicionar, deixe a parte mais longa à direita (no exemplo, ao dividir em dois 88.209, formam-se dois grupos: um com dois dígitos e outro com três, portanto, seguindo as indicações, quando separadas, ficam como 88 e 209 e não 882 e 09).