Três grandes matemáticos árabes que fizeram importantes descobertas para a ciência

Para pesquisadores da Universidade de St. Andrews, no Reino Unido, "a matemática estudada atualmente tem estilo muito mais próximo da contribuição árabe/islâmica que dos gregos".

"Nem a matemática nem a física moderna existiriam sem a álgebra. Não haveria computadores sem algoritmos, nem química sem alcalinos", segundo o físico teórico Jim Al-Khalili.

Al-Khalili, professor da Universidade de Surrey, no Reino Unido, produziu o documentário da BBC Science and Islam ("A ciência e o Islã", em tradução livre).

Relacionadas

O professor que inspirou criatividade matemática de Stephen Hawking

Cientistas dizem ter descoberto a 'fórmula matemática da forma dos ovos'

Receba notícias de Tilt no WhatsApp e no Telegram

"A linguagem da ciência moderna ainda tem muitas referências às suas raízes árabes", destacou ele no programa de TV. "Do século 12 até o 17, pesquisadores europeus faziam referências frequentes a textos islâmicos do passado."

E mostra uma cópia do Liber Abbaci ("O livro do cálculo", em tradução livre) de Leonardo de Pisa, mais conhecido como Fibonacci, que se tornaria o primeiro grande matemático da Europa medieval.

"O fascinante é que, na página 406, existe uma referência a um texto antigo chamado Modum algebre et almuchabale e, nas suas margens, está escrito o nome Maumeht — a versão latinizada do nome árabe Mohammed", segundo Al-Khalili.

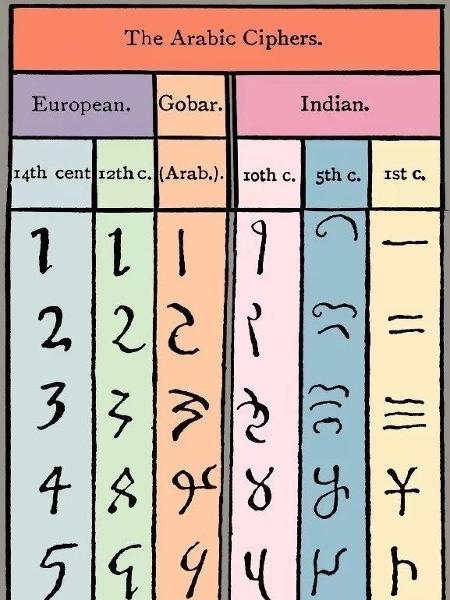
Tratava-se de Abu Abdallah Muḥammad ibn Musa al-Jwarizmi, cujo nome ocidental é Al-Khwarizmi (Al-Cuarismi, em português), que derivou na palavra algoritmo. Ele viveu aproximadamente entre os anos 780 e 850. Al-Cuarismi descreveu a ideia revolucionária de que é possível representar qualquer número desejado com apenas 10 símbolos simples.

Esse grande matemático, que emigrou da Pérsia oriental para Bagdá (hoje, capital do Iraque), deu ao Ocidente os números e o sistema decimal. É frequentemente designado o pai da álgebra.

"Agora se sabe que muitas das ideias que antes se imaginava que fossem conceitos novos e brilhantes graças aos matemáticos europeus dos séculos 16, 17 e 18 foram desenvolvidas por matemáticos árabes/islâmicos cerca de quatro séculos antes", segundo John Joseph O'Connor e Edmund Frederick Robertson, da Universidade de St. Andrews, no Reino Unido.

Para eles, "em muitos aspectos, a matemática estudada atualmente tem estilo muito mais próximo da contribuição árabe/islâmica que dos gregos".

Ao longo da história, houve grandes matemáticos no mundo árabe e islâmico. Aqui apresentamos três deles.

Al-Batani

Para Juan Martos Quesada, professor aposentado e ex-diretor do Departamento de Estudos Árabes e Islâmicos da Universidade Complutense de Madri, na Espanha, uma das principais contribuições dos matemáticos árabes "foi resgatar a ciência grega e latina com suas traduções".

Mas eles também recuperaram o melhor da ciência desenvolvida pelos indianos. "A grande importância de Al-Batani foi ter conseguido unir a astronomia e a matemática, compondo um único campo de estudo", segundo declarou Martos Quesada à BBC News Mundo, serviço em espanhol da BBC.

"Ele aplicou muitas fórmulas matemáticas à astronomia. Determinou com grande precisão, por exemplo, o ano solar com 365 dias — o que foi um grande feito, já que estamos falando em finais do século 9 e início do século 10."

"Com relação aos equinócios, ele os estudou e concluiu que havia erros nas contas feitas por Ptolomeu. Isso serviu para aperfeiçoar toda a herança grega de Ptolomeu que foi recebida pelos matemáticos árabes", segundo Martos Quesada. Al-Batani também estabeleceu uma série de relações trigonométricas.

Para o documentário da BBC, Al-Khalili visitou a Universidade de Pádua, na Itália, e viu um dos livros mais importantes da história da ciência: De revolutionibus orbium coelestium ("Sobre a revolução das esferas celestes", em tradução livre), publicado em 1543 por Nicolau Copérnico.

"A importância desse livro é enorme", ressalta Al-Khalili. "Nele, Copérnico defende pela primeira vez, desde a antiguidade grega, que todos os planetas, incluindo a Terra, giram ao redor do sol. Muitos historiadores o consideram o iniciador da revolução científica europeia."

Copérnico menciona o astrônomo Machometi Aracenfis, que é o grande Al-Batani.

"É para mim uma grande revelação que ele mencione explicitamente um muçulmano do século 9, que forneceu muitas informações sobre suas observações", ressalta Al-Khalili. "Copérnico usou extensamente as observações de Al-Batani sobre a posição dos planetas, do sol, da lua e das estrelas."

Al-Batani nasceu em 858 perto de Urfa, na Síria, e morreu em 929, no Iraque.

Jaime Coullaut Cordero, professor de estudos árabes e islâmicos da Universidade de Salamanca, na Espanha, conversou com a BBC News Mundo sobre Ibn Al-Shatir, astrônomo e matemático que nasceu em Damasco, hoje capital da Síria, perto do ano de 1304.

"Ele foi pouco conhecido no Ocidente porque suas obras não foram traduzidas para o latim", segundo Cordero. Mas ele ressalta que, nos anos 1980, "pesquisadores descobriram os modelos planetários de Ibn Al-Shatir e perceberam que eram iguais aos modelos propostos por Copérnico alguns séculos depois".

Al-Hazém

Shaikh Mohammad Razaullah Ansari, professor emérito de física da Universidade Muçulmana de Aligarh, na Índia, escreveu um artigo para a página da Unesco sobre um erudito árabe dos séculos 10° e 11 que se dedicou não só à matemática, mas também à física, mecânica, astronomia, filosofia e medicina.

Trata-se do grande Abu Ali al-Ḥasan Ibn al-Haytham al-Basri, cujo nome em português é Al-Hazém. Ele nasceu no Iraque no ano 965 e morreu no Egito em 1040. Foi um dos famosos cientistas do Cairo, no Egito, e chamado de "segundo Ptolomeu" pelos eruditos árabes.

Al-Hazém é considerado o pai do método científico moderno. Ele desenvolveu a metodologia de "experimentação como outra forma de comprovar a hipótese ou premissa básica", segundo Razaullah Ansari.

Já Martos Quesada destaca suas contribuições para os princípios da óptica. De fato, Razaullah Ansari ensina que sua obra mais famosa foi sobre a óptica: Kitab fi al-Manazir, traduzido de forma anônima para o latim nos séculos 12 e 13 com o título Opticae Thesaurus ("O livro da óptica", em tradução livre). Em sete volumes, Al-Hazém estudou as propriedades da luz, de forma experimental e matemática.

Mas Al-Hazém foi também um grande matemático, como explica Ricardo Moreno, escritor e professor da faculdade de matemática da Universidade Complutense na página do Centro Virtual de Divulgação da Matemática.

"Ele foi um dos primeiros matemáticos árabes a estudar com sucesso equações de grau superior ao segundo, quando resolveu geometricamente uma equação de terceiro grau proposta por Arquimedes, mais de 1.200 anos antes, na sua obra Sobre a Esfera e o Cilindro", segundo Moreno.

No campo da teoria dos números, Al-Hazém deixou contribuições importantes com seu trabalho sobre os números perfeitos. Ele também desenvolveu a geometria elementar e pesquisou casos específicos dos teoremas de Euclides.

Abu Kamil

Ricardo Moreno destaca que a morte de Al-Cuarismi "coincidiu aproximadamente com o nascimento, no Egito, de Abu Kamil ibn Aslam ibn Mohammed, conhecido como o calculista egípcio".

"Ele viveu 80 anos e deixou inúmeras obras matemáticas — entre elas, um tratado de álgebra, cujo original em árabe se perdeu, mas do qual duas traduções chegaram até nós, uma em latim e outra em hebraico. Ele resolve equações de segundo grau de forma geométrica, como seu predecessor de Bagdá, mas apoiado mais diretamente nos Elementos [de Euclides]", segundo Moreno.

Uma breve biografia de O'Connor e Robertson indica que se sabe muito pouco sobre a vida de Abu Kamil — mas o suficiente para compreender seu papel no desenvolvimento da álgebra. Segundo os autores, "Kamil foi um dos sucessores imediatos de Al-Cuarismi". E, de fato, o próprio Kamil destaca o papel de Al-Cuarismi como o "inventor da álgebra".

"Mas existe outra razão para a importância de Abu Kamil: seu trabalho foi a base dos livros de Fibonacci", segundo O'Connor e Robertson. "Kamil é importante não apenas no desenvolvimento da álgebra árabe, mas também porque, através de Fibonacci, tem importância fundamental na introdução da álgebra na Europa."