Estudante canadense refaz cálculo clássico de viagem pelo interior da Terra

Se a viagem à lua contada por Júlio Verne em 1865 se tornou realidade, quem sabe um dia a viagem ao centro da Terra, tema de um dos seus livros mais famosos, também venha a acontecer. Por enquanto, ainda é um problema clássico proposto a estudantes de Física: se fosse possível cavar um túnel passando pelo centro da Terra, quanto tempo demoraria a viagem até o outro lado? A resposta por décadas foi 42 minutos e 12 segundos.

Entretanto, o estudante Alexander Klotz, da Universidade de McGill, em Montreal, no Canadá refez os cálculos e chegou a um outro resultado:  38 minutos e 11 segundos. A pesquisa foi publicada no American Journal of Physics. “A resposta clássica considera condições ideais, como partir do pressuposto de que a Terra é esférica, enquanto o formato se aproxima mais de uma laranja, achatada nos pólos, explica Ítalo Curcio, físico e professor da Universidade Mackenzie.

Assume-se ao mesmo tempo que a densidade do planeta é uniforme, mas a Terra não possui a mesma densidade em todas suas camadas. A crosta tende a ser menos densa que o interior. Levar isso em conta foi a novidade do cálculo de Klotz. Para conseguir uma distribuição mais realista da massa do planeta, ele se baseou no Modelo Preliminar de Referência da Terra, feito a partir de dados sísmicos. Foi por meio de ondas sísmicas que surgiram as primeiras evidências da existência de um manto terrestre, ou seja, a segunda camada depois da crosta e anterior ao núcleo do globo. Em densidades diferentes, a força da gravidade age de forma diversa.

O problema do suposto túnel é proposto a estudantes de Física para demonstrar a lei da gravidade e um tipo importante de movimento. “Se abandonássemos uma bola numa das extremidades deste túnel, ela ganharia velocidade até o centro e perderia velocidade depois. Iria e voltaria indefinidamente de um lado ao outro", explica Curcio.

Ele também avisa que ainda não conhecemos toda a estrutura interna do planeta. Assim, embora seja mais próximo da realidade, o novo cálculo ainda não é preciso. O editor da publicação americana, o físico David Jackson, da Faculdade Dickinson em Carlisle, Pensilvânia, acrescenta que o interessante de tudo isso é que se pode substituir uma afirmação hipotética por outra e ainda assim conseguir uma resposta muito mais correta.

Voltando à viagem ao centro da Terra, a distância seria de 6.400 quilômetros para chegar ao ponto central e 12.800 quilômetros para sair do outro lado. “Para comparar, a profundidade perfurada para se chegar ao pré-sal, que fica abaixo de uma camada de rocha da crosta, é de 5 a 7 quilômetros”, diz Curcio.

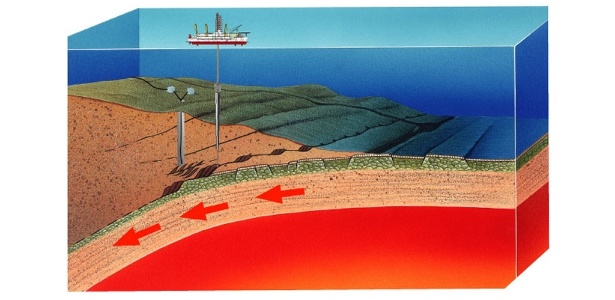
Uma equipe internacional de cientistas tenta levar uma sonda ao manto terrestre. Em setembro de 2012, o Programa Integrado para a Escavação do Oceano (IODP) conseguiu perfurar 2,446 quilômetros no litoral do Japão e pretende chegar a 6 quilômetros em 2020, onde atingiria o manto e poderia-se desvendar mistérios sobre a formação do planeta.

Os desafios são grandes: a perfuração deve ser feita a partir de um barco no Oceano, pois o fundo do mar está mais próximo do manto e as brocas precisam ser muito resistentes, pois as rochas a serem perfuradas são muito duras. Mesmo sendo feitas de uma mistura de carbeto de tungstênio (material três vezes mais rígido que o aço) e diamante, aguentam apenas 60 horas de trabalho.

Já para chegar ao centro da Terra são necessários milhares de quilômetros. “A ciência vive de hipóteses e sonhos. O homem não sonhou voar e falar à distância? Os sonhos se realizam, é uma questão de tempo”, lembra o físico brasileiro.